FWL Theorem and Double Machine Learning¶

Following up on the previous notebook where we covered several doubly robust methods (e.g., AIPW and TMLE), we will go through double machine learning (DML) in detail in this notebook. But before diving into theory let us understand why we need DML in the first place, shall we?

Augmented inverse propensity weighting (AIPW) is a modification of the inverse propensity weighting (IPW) that guarantees double roubustness and consistent average treatment effect(ATE) estimate even if 1) treatment/exposure model ($ \hat\pi(x) $) or 2) outcome model ($ \hat\mu(x) $) is misspecified GLynn and Quinn, 2009. Although AIPW provides a nice flexibility in estimating a consistent ATE, it does necessitate at least one model to be correctly specified. If both the models are incorrectly specified, the naive IPW outperforms AIPW. Similarly, targeted maximum likelihood estimation (TMLE) is a semiparametric estimation framework. TMLE tends to work well when the treatment is not a weak predictor of the outcome. If that’s not the case, the estimation tends to be biased toward zero which obviously might not be the baseline truth.

The main objective of DML is to provide a general framework to estimating and performing inference on low-dimensional parameter ($ \theta_0$) in presence of high-dimensional nuisance parameter utilizing nonparametric machine learning methods. DML works for both binary and continuous treatment variables which is not the case for some of the doubly robust methods. As the name suggests, DML leverages “double” or two high-performance ML methods to estimate a high-quality $\theta_0$. Specifically, the first ML algorithm is used for treatment model while the second algorithm is used for the outcome model. Finally, Frisch-Waugh-Lovell (FWL)-type residuals-on-residuals regressioin is utilized to get a de-biased estimate of $\theta_0$. DML is also know as “debiased-ML” or “orthogonalized ML.”

FWL Theorem/Orthogonalization¶

Orthogonalization (or equivalently FWL Theorem (Frisch and Waugh, 1933; Lovell, 1963) is the backbone of DML. Its principled approach guarantees an unbiased estimate. Since it is a key to understanding why DML works, we will first prove the FWL Theorem and implement it in an example to demonstrate how it debiases the data before moving on to the details of DML.

Let us take a multivariate linear regression $$ Y = D_1\beta_1 + X\beta_2 + \epsilon $$ where $Y$ is $ n \times 1$ outcome, $D$ is $n \times p_1$ treatment variables, and $X$ is $n \times p_2$ covariates or nuisance parameters.

Multiply the equation with residual maker function ($G$) of the treatment parameters $D$. The residual maker is defined by $Gy = y - D(D'D)^{-1}D'y \equiv y - D\beta \equiv \epsilon_D$

\[ GY = GD_1\beta_1 + GX\beta_2 + G\epsilon \]

Since $GD_1\beta_1 \equiv 0$, the equation above simplifies to

\[ GY = GX\beta_2 + G\epsilon \]

Now, the final equation becomes

\[ GY = GX\beta_2 + \epsilon \]

Taking a closer look at the equation, we can see that we are regressing residuals on residuals. This shows that results obtained from multivariate linear regression is the same as the residuals-on-residuals regression.

Now that we have seen a proof of why residuals-on-residuals regression work, let us go through an example implementation to see orthogonalization in action.

# importing required packages
import os
from joblib import Parallel, delayed
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
import statsmodels.api as sm

import doubleml as dml
from doubleml.datasets import fetch_401K

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV, LogisticRegressionCV, LinearRegression, LogisticRegression
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import train_test_split

from xgboost import XGBClassifier, XGBRegressor

plt.rcParams["font.family"] = "Times New Roman"
plt.rcParams['xtick.labelsize'] = 14
plt.rcParams['ytick.labelsize'] = 14
plt.rcParams['figure.figsize'] = 10., 6

Orthogonalization: Example¶

To demonstrate how orthogonalization debiases the data, we will use a simulated data on ice cream sales. The outcome ($Y$) is the number of sales, the treatment is price, and the covariates ($X$) are temperature, weekday (categorical variable) and cost of the ice cream.

df_ortho = pd.read_csv('ice_cream_sales.csv')
df_ortho.head()

	temp	weekday	cost	price	sales
0	17.3	6	1.5	5.6	173
1	25.4	3	0.3	4.9	196
2	23.3	5	1.5	7.6	207
3	26.9	1	0.3	5.3	241
4	20.2	1	1.0	7.2	227

There are no missing data as we can see below:

df_ortho.isna().sum()

temp       0
weekday    0
cost       0
price      0
sales      0
dtype: int64

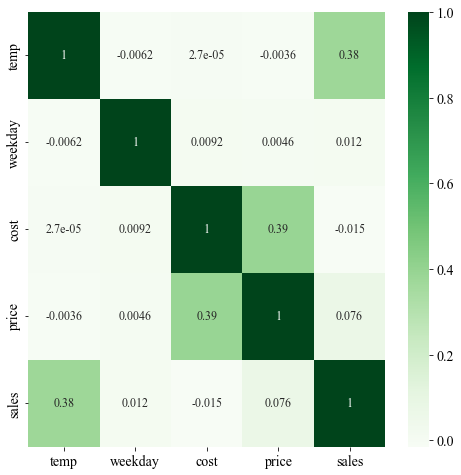
The figure below shows a heatmap of the Pearsons’ correlation plot of the dataset. The correlation plot shows positive linear relationship between three pairs of variables (sales-temp, cost-price, and price-sales)- two of which makes sense, one does not. As the temperature increases, we often expect ice cream sales to increase because people buy more ice cream if it is hot. Similarly, the price of the ice crease will increase if the purchase cost for the vendor is high. However, the third positive correlation is between price and sales which necessarily doesn’t make sense because if the price is high, people tend to buy less so if anything, there should be a negative correlation. The positive correlation could potentially because of bias.

plt.figure(figsize=(8,8))
sns.heatmap(df_ortho.corr(), cmap="Greens",annot=True, annot_kws={"fontsize":'large'})
# plt.savefig('corr_plot_iceCream.png', bbox_inches='tight')
plt.show()

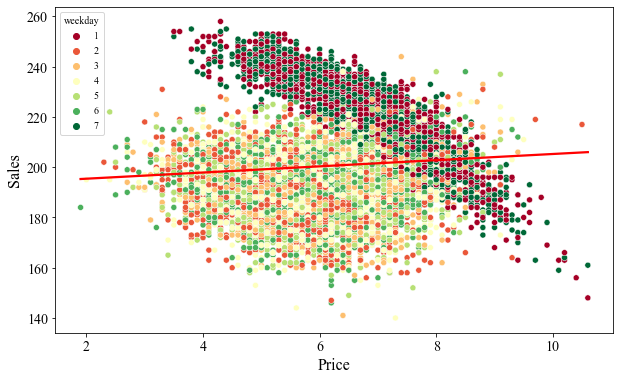
Looking at the scatter plot between sales and price, we can see that the data clearly is biased. First, we can see the two distinct cluster. On weekends, the sales is high because more people go outside which increases the demand. The vendors likely take an advantage of the increased demands and hike up the prices which ultimately reduces the sales. However, the sales appear to be roughly uniform regardless of the price during weekdays. The higher sales on weekends and the consistent sales during weekdays gives a positive relationship between sales and price as shows by a linear fit line (red line) in the figure below.

plt.figure()
sns.scatterplot(data=df_ortho, x="price", y="sales", hue="weekday", palette='RdYlGn', legend='full');
sns.regplot(x='price', y='sales', data=df_ortho, scatter=False, ci=False, color ='red')
plt.xlabel('Price', fontsize=16)
plt.ylabel('Sales', fontsize=16)
# plt.savefig('scatter_original_iceCream.png', bbox_inches='tight')
plt.show()

To debiase the data, we need two models- treatment and outcome model. The treatment model debiases the bias induced in price using all the other confounders, while the outcome model debiases the bias in sales introduced by the same covariates. Consistent with FWL Theorem, we used OLS to create the treatment and outcome models as shown below:

#create a treatment model 
model_treatment = smf.ols("price ~ cost + C(weekday) + temp", data=df_ortho).fit()
#create an outcome model
model_outcome = smf.ols("sales ~ cost + C(weekday) + temp", data=df_ortho).fit()

debiased_df_ortho = df_ortho.assign(**{"resid_output_sales":model_outcome.resid,
                                       'resid_treatment_price':model_treatment.resid})

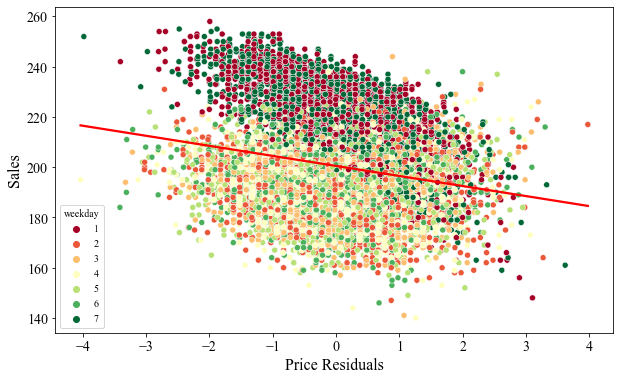
If we plot price-residuals against sales, we can see that we have debiased the bias in price. First, we have uncovered the negative relationship between the price and sales as expected. Most importantly, we can see that decline in sales during the weekend is consistent and not necessarily depending on the price. In the raw data above, we saw that as the price increased, the sales decreased drastically, thus inducing price bias. But in this case, the number of sales on the left and the right side of price-residual roughly appears to be the same.

Even though we have debiased the price, we can still see that the data has two distinct clusters as a function of the sale day. During weekends, the sales seems to be higher as compared to the weekdays.

plt.figure()
sns.scatterplot(data=debiased_df_ortho, x="resid_treatment_price", y="sales",
                hue="weekday", palette='RdYlGn', legend='full')
sns.regplot(x='resid_treatment_price', y='sales', data=debiased_df_ortho, scatter=False, ci=False, color ='red')
plt.xlabel('Price Residuals', fontsize=16)
plt.ylabel('Sales', fontsize=16)
# plt.savefig('scatter_priceDebiased_iceCream.png', bbox_inches='tight')
plt.show()

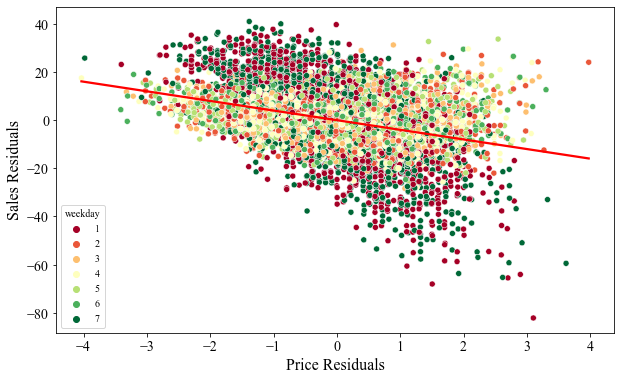
Finally, lets see if we can debiase the bias in sales amount. The figure below plots sales-residuals against price-residuals. We can see that the we no longer have distinct clusters of data neither do we see a dramatic decline in sales as the price increase. The slope of the linear fit line (red line) is the debiased estimated of ATE that is obtained by regressing price-residuals on sales-residuals.

plt.figure()
sns.scatterplot(data=debiased_df_ortho, x="resid_treatment_price", y="resid_output_sales",
                hue="weekday", palette='RdYlGn', legend='full')
sns.regplot(x='resid_treatment_price', y='resid_output_sales', data=debiased_df_ortho,
            scatter=False, ci=False, color ='red')
plt.xlabel('Price Residuals', fontsize=16)
plt.ylabel('Sales Residuals', fontsize=16)
# plt.savefig('scatter_doubleDebiased_iceCream.png', bbox_inches='tight')
plt.show()

This example illustrates the role orthogonalization playing in debiasing the data and more importantly estimating a debiased ATE estimate.

Debiased/Double Machine Learning¶

Now that we understand orthogonalization, we will dig a little deeper into DML formulations. Good news is that if you understand the intuition behind orthogonalization, you already understand DML. To simplify, DML is fundamentally the same as orthogonalization except that advanced ML algorithms are used to model treatment and outcome instead of OLS.

One may wonder, ML algorithms are widely used in anything and everything, haven’t researchers used to estimate treatment effect? Yes, they have and that’s when naive approach comes in. In this section, naive approach refers to methods involving ML methods with no modifications. Since DML is a slighly different class of roubly-robust method in a sense that it utilized ML algorith, we introduce Naive or prediction-based ML approach to make a direct comparison against DML and show why DML is better than the naive approach.

To be consistent with the Double/Debiased Machine Learning Paper(Chernozhukov et al., 2018), we will use the same notations.

Let us take a partial linear regression, $$Y = D\theta_0 + g_0(X) + U, \quad E[U|X, D] = 0 $$

\[D = m_0(X) + V, \quad E[V|X] = 0\]

where $Y$ is the outcome, $D$ is the treatment, $X$ is the covariates/confounders, and $U$ and $V$ are the noise. The quantity of interest is the regression coefficient, $\theta_0$.

Under naive approach, the following steps are undertaken to estimate the $\theta_0$

Predict $Y$ using $D$ and $X$. This gives you $\hat Y$ in the form of $D\hat\theta_0 + \hat g_0(X)$
Run advanced ML algorithm (e.g., Random Forest) of $Y - D\hat\theta_0$ on $X$ to fit $\hat g_0(X)$
Run OLS of $Y - \hat g_0(X)$ on $D$ to fit $\hat\theta_0$. In other words, $\hat\theta_0$ is given by:

\[ \hat\theta_0 = \left( \frac{1}{n} \sum_{i \in I} D_i^2 \right)^{-1} \frac{1}{n} \sum_{i \in I}D_i(Y_i - \hat g(X_i)) \]

The naive approach displays excellent predictive performance but introduces a regularization bias in learning $g_0$. Lets take a closer look at the decomposition of the estimation error in $\hat\theta_0$ to islolate the regularization bias,

\[\sqrt{n}(\hat\theta_0 - \theta_0) = \underbrace{\left( \frac{1}{n} \sum_{i \in I} D_i^2 \right)^{-1} \frac{1}{\sqrt{n}} \sum_{i \in I} D_i U_i}_{:a} + \underbrace{\left( \frac{1}{n} \sum_{i \in I} D_i^2 \right)^{-1} \frac{1}{\sqrt{n}} \sum_{i \in I} D_i(g_0(X_i) - \hat g_0(X_i))}_{:b}\]

The first term $a$ is well-behaved under mild conditions and has zero mean $a \rightsquigarrow N(0, \bar\Sigma)$ for some $\bar\Sigma$. However, the regularization term ($b$) does not center around 0, and in fact diverges for the majority of the ML algorithms. The regularization bias is addressed using orthogonalization. How exactly does DML do it? Using the following three steps:

Predict $Y$ and $D$ using $X$ using the advanced ML methods to obtain $\widehat{E[Y|X]}$ and $\widehat{E[D|X]}$
Obtain residuals from the two models i.e. $\widehat{W} = Y -\widehat{E[Y|X]}$ and $\widehat{V} = D -\widehat{E[D|X]}$
Use orthogonalization, i.e. regress $\widehat{W}$ on $\widehat{V}$ to get $\hat\theta_0$

In DML, the estimation error in $\hat\theta_0$ can be decomposed into

\[\sqrt{n}(\hat\theta_0-\theta_0) = a^* + b^* + c^*\]

where, $$a^* = (EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}V_iU_i \rightsquigarrow N(0, \Sigma),$$

\[b^* = (EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}(\hat m_0(X_i) - m_0(X_i))(\hat g_0(X_i) - g_0(X_i)) \]

and,

\[ c^* = o_P(1)\]

Similar to naive approach, $a^*$ has a zero mean. The second term, $b^*$ also nearly as zero mean because the the high predictive performance of advanced ML algorithms ensure that the product of the estimation error in $\hat m_0$ and $\hat g_0$ nearly vanishes to zero. The $c^*$ term represents bias induced due to overfitting, which is sufficiently well-behaved and vanishes in probability under sample splitting. For DML to be doubly robust, it is paramount to split the data into multiple folds while estimating $\hat\theta_0$. For a detailed proof on why $c^*$ vanishes in probability in presence of sample splitting, we invite readers to read the Double/Debiased Machine Learning Paper.

DML: Example Implementation¶

In this example, we will use the data on 401(k) eligibility (treatment variable) on the total accumulated net financial assess (net_tfa). This dataset was assembled from the 1991 Survey of Income and Porgram Participation. Since the assignment was not random, the DML is implemented to negate bias due to non-randomness assignment.

df_401k = fetch_401K(return_type='DataFrame')
df_401k.sample(n=5)

	nifa	net_tfa	tw	age	inc	fsize	educ	db	marr	twoearn	e401	p401	pira	hown
6174	8000.0	15000.0	49500.0	33	50751.0	4	16	0	1	0	0	0	1	1
6570	35000.0	72000.0	222000.0	38	102396.0	1	16	1	0	0	1	1	1	1
9196	13499.0	13499.0	21960.0	31	24750.0	1	16	0	0	0	1	0	0	0
2127	500.0	-250.0	-250.0	33	24114.0	3	9	0	1	1	0	0	0	0
835	6400.0	10100.0	12675.0	26	30342.0	1	15	0	0	0	0	0	1	0

The description of the features are highlighted below:

age: age of the employee
inc: income amount
fsize: family size
educ: years of education
marr: marriage indicator (1: married, 0: otherwise)
twoearn: two-earner status indicator in the family
db: a defined benefit pension status indicator
pira: an IRA participation indicator
hown: a home ownership indicator
net_tfa: net total financial assets. Defined as the sum fo IRA balances, 401(k) balances, checking accounts, U.S. saving bonds, stocks, mutual funds, etc.

As discussed below, we will not use all of the features in this example.

df_401k.shape

(9915, 14)

Difference in mean between the employees who were eligible vs not eligible.

df_401k.groupby('e401')['net_tfa'].mean()

e401
0    10788.044922
1    30347.388672
Name: net_tfa, dtype: float32

Difference in mean between the employees who opted to participate in 401(k) vs those that did not participate.

df_401k.groupby('p401')['net_tfa'].mean()

p401
0    10890.477539
1    38262.058594
Name: net_tfa, dtype: float32

For consistency, we will use the same covariates used in the Double/Debiased Machine Learning Paper.

features_cherno = [ 'age', 'inc', 'fsize', 'educ', 'marr', 'twoearn', 'db', 'pira', 'hown']

#outcome model 
my = smf.ols('net_tfa ~ ' + '+'.join(features_cherno), data = df_401k).fit()

#treatment model
mt = smf.ols('e401 ~  ' + '+'.join(features_cherno), data = df_401k).fit()

One of the limitations we have not mentioned before is that the orthogonalization is limited to linear relationship between the covariates, treatment, and outcome models. Of course, the linear regression can be extended to a polynomial regression to capture nonlinear relationship but having to specify the nonlinear functional form is not that flexible and desirable. We implement linear and polynomial regression to shed light on the high-level predictive performance of commonly used ML algorithms.

orthogonal = smf.ols("tfa_res~e401_res", 
        data=df_401k.assign(tfa_res=my.resid, # sales residuals
                          e401_res=mt.resid) # price residuals
       ).fit()
orthogonal.summary().tables[1]

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	1.527e-09	559.394	2.73e-12	1.000	-1096.527	1096.527
e401_res	5896.1984	1249.446	4.719	0.000	3447.029	8345.367

## creating a dummy dataframe for easy data parsing 
dummydf = pd.DataFrame(orthogonal.summary().tables[1])

d = {'coef': orthogonal.params['e401_res'],
     'std err':dummydf[2][2],
     '2.5 %':dummydf[5][2],
     '97.5 %':dummydf[6][2]}
df_linear = pd.DataFrame([d])
df_linear.head()

	coef	std err	2.5 %	97.5 %
0	5896.198421	1249.446	3447.029	8345.367

Creating a polynomial regression

my_poly = smf.ols('net_tfa ~ age + inc + educ + fsize + marr + twoearn + db + pira + hown + age*fsize + educ*age + fsize**2',
                  data = df_401k).fit()
mt_poly = smf.ols('e401 ~ age + inc + educ + fsize + marr + twoearn + db + pira + hown', data = df_401k).fit()

polynomial = smf.ols("tfa_res~e401_res", 
        data=df_401k.assign(tfa_res=my_poly.resid, # sales residuals
                          e401_res=mt_poly.resid) # price residuals
       ).fit()

As we can see, for the polynomial regression, the estimated ATE is slighly higher by about $200 as compared to OLS. This indicates that the data is highly nonlinear and we can leverage the ML algorithms to capture the nonlinear relationship.

dummydf = pd.DataFrame(polynomial.summary().tables[1])

d = {'coef': polynomial.params['e401_res'],
     'std err':dummydf[2][2],
     '2.5 %':dummydf[5][2],
     '97.5 %':dummydf[6][2]}
df_polynomial = pd.DataFrame([d])
df_polynomial.head()

	coef	std err	2.5 %	97.5 %
0	6084.770503	1247.310	3639.789	8529.752

# Initialize DoubleMLData (data-backend of DoubleML)
data_dml_base = dml.DoubleMLData(df_401k,
                                 y_col='net_tfa',
                                 d_cols='e401',
                                 x_cols=features_cherno)

In the following section, Random Forest, Xtreme Gradient Boosting (XGBoost), and Regression trees are implemented to estimate the ATE in terms of the total financial asset. Two variations of implementation are provided (3 folds and 5 folds data splits) to highlight the role sample spliting plays in reducing the bias.

# Random Forest with 3 folds split
randomForest = RandomForestRegressor(
    n_estimators=500, max_depth=7, max_features=3, min_samples_leaf=3)
randomForest_class = RandomForestClassifier(
    n_estimators=500, max_depth=5, max_features=4, min_samples_leaf=7)

np.random.seed(123)
dml_plr_forest = dml.DoubleMLPLR(data_dml_base,
                                 ml_g = randomForest,
                                 ml_m = randomForest_class,
                                 n_folds = 3, 
                                n_rep=10)
dml_plr_forest.fit(store_predictions=True)
forest_summary3 = dml_plr_forest.summary

forest_summary3

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
/var/folders/3_/kmdwwvws6jd6jbgwvk49zrfc0000gn/T/ipykernel_6980/3586736964.py in <module>
     11                                  n_folds = 3,
     12                                 n_rep=10)
---> 13 dml_plr_forest.fit(store_predictions=True)
     14 forest_summary3 = dml_plr_forest.summary
     15 

~/opt/miniconda3/lib/python3.8/site-packages/doubleml/double_ml.py in fit(self, n_jobs_cv, keep_scores, store_predictions)
    475                 # ml estimation of nuisance models and computation of score elements
    476                 self._psi_a[:, self._i_rep, self._i_treat], self._psi_b[:, self._i_rep, self._i_treat], preds =\
--> 477                     self._nuisance_est(self.__smpls, n_jobs_cv)
    478 
    479                 if store_predictions:

~/opt/miniconda3/lib/python3.8/site-packages/doubleml/double_ml_plr.py in _nuisance_est(self, smpls, n_jobs_cv)
    151 
    152         # nuisance m
--> 153         m_hat = _dml_cv_predict(self._learner['ml_m'], x, d, smpls=smpls, n_jobs=n_jobs_cv,
    154                                 est_params=self._get_params('ml_m'), method=self._predict_method['ml_m'])
    155         _check_finite_predictions(m_hat, self._learner['ml_m'], 'ml_m', smpls)

~/opt/miniconda3/lib/python3.8/site-packages/doubleml/_utils.py in _dml_cv_predict(estimator, x, y, smpls, n_jobs, est_params, method, return_train_preds)
     98         if est_params is None:
     99             # if there are no parameters set we redirect to the standard method
--> 100             preds = cross_val_predict(clone(estimator), x, y, cv=smpls, n_jobs=n_jobs, method=method)
    101         else:
    102             assert isinstance(est_params, dict)

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/model_selection/_validation.py in cross_val_predict(estimator, X, y, groups, cv, n_jobs, verbose, fit_params, pre_dispatch, method)
    961     # independent, and that it is pickle-able.
    962     parallel = Parallel(n_jobs=n_jobs, verbose=verbose, pre_dispatch=pre_dispatch)
--> 963     predictions = parallel(
    964         delayed(_fit_and_predict)(
    965             clone(estimator), X, y, train, test, verbose, fit_params, method

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in __call__(self, iterable)
   1044                 self._iterating = self._original_iterator is not None
   1045 
-> 1046             while self.dispatch_one_batch(iterator):
   1047                 pass
   1048 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in dispatch_one_batch(self, iterator)
    859                 return False
    860             else:
--> 861                 self._dispatch(tasks)
    862                 return True
    863 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in _dispatch(self, batch)
    777         with self._lock:
    778             job_idx = len(self._jobs)
--> 779             job = self._backend.apply_async(batch, callback=cb)
    780             # A job can complete so quickly than its callback is
    781             # called before we get here, causing self._jobs to

~/opt/miniconda3/lib/python3.8/site-packages/joblib/_parallel_backends.py in apply_async(self, func, callback)
    206     def apply_async(self, func, callback=None):
    207         """Schedule a func to be run"""
--> 208         result = ImmediateResult(func)
    209         if callback:
    210             callback(result)

~/opt/miniconda3/lib/python3.8/site-packages/joblib/_parallel_backends.py in __init__(self, batch)
    570         # Don't delay the application, to avoid keeping the input
    571         # arguments in memory
--> 572         self.results = batch()
    573 
    574     def get(self):

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in __call__(self)
    260         # change the default number of processes to -1
    261         with parallel_backend(self._backend, n_jobs=self._n_jobs):
--> 262             return [func(*args, **kwargs)
    263                     for func, args, kwargs in self.items]
    264 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in <listcomp>(.0)
    260         # change the default number of processes to -1
    261         with parallel_backend(self._backend, n_jobs=self._n_jobs):
--> 262             return [func(*args, **kwargs)
    263                     for func, args, kwargs in self.items]
    264 

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/utils/fixes.py in __call__(self, *args, **kwargs)
    209     def __call__(self, *args, **kwargs):
    210         with config_context(**self.config):
--> 211             return self.function(*args, **kwargs)
    212 
    213 

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/model_selection/_validation.py in _fit_and_predict(estimator, X, y, train, test, verbose, fit_params, method)
   1043         estimator.fit(X_train, **fit_params)
   1044     else:
-> 1045         estimator.fit(X_train, y_train, **fit_params)
   1046     func = getattr(estimator, method)
   1047     predictions = func(X_test)

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/ensemble/_forest.py in fit(self, X, y, sample_weight)
    440             # parallel_backend contexts set at a higher level,
    441             # since correctness does not rely on using threads.
--> 442             trees = Parallel(
    443                 n_jobs=self.n_jobs,
    444                 verbose=self.verbose,

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in __call__(self, iterable)
   1044                 self._iterating = self._original_iterator is not None
   1045 
-> 1046             while self.dispatch_one_batch(iterator):
   1047                 pass
   1048 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in dispatch_one_batch(self, iterator)
    859                 return False
    860             else:
--> 861                 self._dispatch(tasks)
    862                 return True
    863 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in _dispatch(self, batch)
    777         with self._lock:
    778             job_idx = len(self._jobs)
--> 779             job = self._backend.apply_async(batch, callback=cb)
    780             # A job can complete so quickly than its callback is
    781             # called before we get here, causing self._jobs to

~/opt/miniconda3/lib/python3.8/site-packages/joblib/_parallel_backends.py in apply_async(self, func, callback)
    206     def apply_async(self, func, callback=None):
    207         """Schedule a func to be run"""
--> 208         result = ImmediateResult(func)
    209         if callback:
    210             callback(result)

~/opt/miniconda3/lib/python3.8/site-packages/joblib/_parallel_backends.py in __init__(self, batch)
    570         # Don't delay the application, to avoid keeping the input
    571         # arguments in memory
--> 572         self.results = batch()
    573 
    574     def get(self):

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in __call__(self)
    260         # change the default number of processes to -1
    261         with parallel_backend(self._backend, n_jobs=self._n_jobs):
--> 262             return [func(*args, **kwargs)
    263                     for func, args, kwargs in self.items]
    264 

~/opt/miniconda3/lib/python3.8/site-packages/joblib/parallel.py in <listcomp>(.0)
    260         # change the default number of processes to -1
    261         with parallel_backend(self._backend, n_jobs=self._n_jobs):
--> 262             return [func(*args, **kwargs)
    263                     for func, args, kwargs in self.items]
    264 

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/utils/fixes.py in __call__(self, *args, **kwargs)
    209     def __call__(self, *args, **kwargs):
    210         with config_context(**self.config):
--> 211             return self.function(*args, **kwargs)
    212 
    213 

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/ensemble/_forest.py in _parallel_build_trees(tree, forest, X, y, sample_weight, tree_idx, n_trees, verbose, class_weight, n_samples_bootstrap)
    170             curr_sample_weight = sample_weight.copy()
    171 
--> 172         indices = _generate_sample_indices(
    173             tree.random_state, n_samples, n_samples_bootstrap
    174         )

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/ensemble/_forest.py in _generate_sample_indices(random_state, n_samples, n_samples_bootstrap)
    126     Private function used to _parallel_build_trees function."""
    127 
--> 128     random_instance = check_random_state(random_state)
    129     sample_indices = random_instance.randint(0, n_samples, n_samples_bootstrap)
    130 

~/opt/miniconda3/lib/python3.8/site-packages/sklearn/utils/validation.py in check_random_state(seed)
   1041         return np.random.mtrand._rand
   1042     if isinstance(seed, numbers.Integral):
-> 1043         return np.random.RandomState(seed)
   1044     if isinstance(seed, np.random.RandomState):
   1045         return seed

KeyboardInterrupt: 

# Random Forest with 5 folds split
randomForest = RandomForestRegressor(
    n_estimators=500, max_depth=7, max_features=3, min_samples_leaf=3)
randomForest_class = RandomForestClassifier(
    n_estimators=500, max_depth=5, max_features=4, min_samples_leaf=7)

np.random.seed(123)
dml_plr_forest = dml.DoubleMLPLR(data_dml_base,
                                 ml_g = randomForest,
                                 ml_m = randomForest_class,
                                 n_folds = 5, 
                                n_rep=10)
dml_plr_forest.fit(store_predictions=True)
forest_summary5 = dml_plr_forest.summary

forest_summary5

	coef	std err	t	P>\|t\|	2.5 %	97.5 %
e401	8961.175025	1309.593551	6.842715	7.770632e-12	6394.418831	11527.931219

# Gradient Boosted Trees with 3 folds split
boost = XGBRegressor(n_jobs=1, objective = "reg:squarederror",
                     eta=0.1, n_estimators=35)
boost_class = XGBClassifier(use_label_encoder=False, n_jobs=1,
                            objective = "binary:logistic", eval_metric = "logloss",
                            eta=0.1, n_estimators=34)

np.random.seed(123)
dml_plr_boost = dml.DoubleMLPLR(data_dml_base,
                                ml_g = boost,
                                ml_m = boost_class,
                                dml_procedure='dml2',
                                n_folds = 3,
                                n_rep = 10)
dml_plr_boost.fit(store_predictions=True)
boost_summary3 = dml_plr_boost.summary

boost_summary3

	coef	std err	t	P>\|t\|	2.5 %	97.5 %
e401	9002.744739	1399.883887	6.431065	1.267127e-10	6259.022737	11746.46674

# Gradient Boosted Trees with 5 folds split
boost = XGBRegressor(n_jobs=1, objective = "reg:squarederror",
                     eta=0.1, n_estimators=35)
boost_class = XGBClassifier(use_label_encoder=False, n_jobs=1,
                            objective = "binary:logistic", eval_metric = "logloss",
                            eta=0.1, n_estimators=34)

np.random.seed(123)
dml_plr_boost = dml.DoubleMLPLR(data_dml_base,
                                ml_g = boost,
                                ml_m = boost_class,
                                dml_procedure='dml2',
                                n_folds = 5,
                                n_rep = 10)
dml_plr_boost.fit(store_predictions=True)
boost_summary5 = dml_plr_boost.summary

boost_summary5

	coef	std err	t	P>\|t\|	2.5 %	97.5 %
e401	8852.014728	1383.993593	6.395994	1.595063e-10	6139.437131	11564.592325

# Regression Decision Trees with 3 folds split
trees = DecisionTreeRegressor(
    max_depth=30, ccp_alpha=0.0047, min_samples_split=203, min_samples_leaf=67)
trees_class = DecisionTreeClassifier(
    max_depth=30, ccp_alpha=0.0042, min_samples_split=104, min_samples_leaf=34)

np.random.seed(123)
dml_plr_tree = dml.DoubleMLPLR(data_dml_base,
                               ml_g = trees,
                               ml_m = trees_class,
                               n_folds = 3, 
                               n_rep = 10)
dml_plr_tree.fit(store_predictions=True)
tree_summary3 = dml_plr_tree.summary

tree_summary3

	coef	std err	t	P>\|t\|	2.5 %	97.5 %
e401	8494.390142	1332.352929	6.375481	1.823902e-10	5883.026386	11105.753898

# Regression Decision Trees with 3 folds split
trees = DecisionTreeRegressor(
    max_depth=30, ccp_alpha=0.0047, min_samples_split=203, min_samples_leaf=67)
trees_class = DecisionTreeClassifier(
    max_depth=30, ccp_alpha=0.0042, min_samples_split=104, min_samples_leaf=34)

np.random.seed(123)
dml_plr_tree = dml.DoubleMLPLR(data_dml_base,
                               ml_g = trees,
                               ml_m = trees_class,
                               n_folds = 5, 
                               n_rep = 10)
dml_plr_tree.fit(store_predictions=True)
tree_summary5 = dml_plr_tree.summary

tree_summary5

	coef	std err	t	P>\|t\|	2.5 %	97.5 %
e401	8365.634772	1319.168039	6.341599	2.273925e-10	5780.112926	10951.156619

ortho_summary = pd.concat((df_linear, df_polynomial))
ortho_summary.index = ['linear', 'polynomial']
plr_summary_3folds = pd.concat(( forest_summary3, tree_summary3, boost_summary3))
plr_summary_3folds.index = [ 'forest', 'tree', 'xgboost']
plr_summary_3folds[['coef','std err', '2.5 %', '97.5 %']]

plr_summary_5folds = pd.concat(( forest_summary5, tree_summary5, boost_summary5))
plr_summary_5folds.index = [ 'forest', 'tree', 'xgboost']
plr_summary_5folds[['coef','std err', '2.5 %', '97.5 %']]

	coef	std err	2.5 %	97.5 %
forest	8961.175025	1309.593551	6394.418831	11527.931219
tree	8365.634772	1319.168039	5780.112926	10951.156619
xgboost	8852.014728	1383.993593	6139.437131	11564.592325

The summary of orthogonalization, DML with 3 folds, and DML with 5 folds sample splits are shown in the dataframe below. We can see that, as we increase the sample splits, the standard error decrease which gives us a tighter confidence bounds and a more robust ATE estimate

df_summary = pd.concat((ortho_summary, plr_summary_3folds,
                        plr_summary_5folds)).reset_index().rename(columns={'index': 'ML'})
df_summary['Model'] = np.concatenate((np.repeat('Orthogonal', 2),
                                      np.repeat('PLR (3 folds)', 3),
                                      np.repeat('PLR (5 folds)', 3)))
df_summary.set_index(['Model', 'ML'])[['coef','std err', '2.5 %', '97.5 %']]

		coef	std err	2.5 %	97.5 %
Model	ML
Orthogonal	linear	5896.198421	1249.446	3447.029	8345.367
Orthogonal	polynomial	6084.770503	1247.310	3639.789	8529.752
PLR (3 folds)	forest	9018.368261	1315.291812	6440.44368	11596.292842
	tree	8494.390142	1332.352929	5883.026386	11105.753898
	xgboost	9002.744739	1399.883887	6259.022737	11746.46674
PLR (5 folds)	forest	8961.175025	1309.593551	6394.418831	11527.931219
	tree	8365.634772	1319.168039	5780.112926	10951.156619
	xgboost	8852.014728	1383.993593	6139.437131	11564.592325

Summary¶

Double Machine Learning (DML) leverages predictive power of advance Machine Learning (ML) algrotighms in estimating heterogeneous treatment effects when all potential confounders are observed and are also high-dimensional. At its core, DML utilizes orthogonalization to address the regularization bias induced by ML algorithm in estimating high-dimensional nuisance parameters. DML requires two ML methods to predict treatment and outcome using the observed covariates. The residuals from the treatment and outcome model is then used to estimate the causal parameter of interest, the treatment effect. The purpose of the treatment residuals is to represent the debiased version of the treatment model because, by definition, residuals are orthogonal to the features used to contruct the model. Similarly, the outcome residuals denoises the outcome model because the outcome residuals can essentially be viewed as a version of the treatment where all the variance from the features are explained. Thus, DML provides a general yet robust framework for estimating and performing inference on treatment/causal variables.

References¶

Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C., Newey, W., & Robins, J. (2018). Double/debiased machine learning for treatment and structural parameters.

Glynn, A. N., & Quinn, K. M. (2010). An introduction to the augmented inverse propensity weighted estimator. Political analysis, 18(1), 36-56.

https://matheusfacure.github.io/python-causality-handbook/22-Debiased-Orthogonal-Machine-Learning.html

https://www.youtube.com/watch?v=eHOjmyoPCFU&t=444s

Bach, P., Chernozhukov, V., Kurz, M. S., and Spindler, M. (2022), DoubleML - An Object-Oriented Implementation of Double Machine Learning in Python, Journal of Machine Learning Research, 23(53): 1-6, https://www.jmlr.org/papers/v23/21-0862.html.

Frisch, R., & Waugh, F. V. (1933). Partial time regressions as compared with individual trends. Econometrica: Journal of the Econometric Society, 387-401.

Lovell, M. C. (1963). Seasonal adjustment of economic time series and multiple regression analysis. Journal of the American Statistical Association, 58(304), 993-1010.

Lovell, M. C. (2008). A simple proof of the FWL theorem. The Journal of Economic Education, 39(1), 88-91.

My sample book

FWL Theorem and Double Machine Learning

Contents